Задача 4342 — Демидович

Указание

Нужно выбрать в качестве локальных координат на цилиндре угол смещённой по оси $z$ полярной системы координат и высоту $y$ .

Найти для новых координат элемент площади и границы $φ$ и $y$ .

Перейти от поверхностного интеграла к повторному.

Решение

Преобразуем уравнение $x^{2} + z^{2} = 2 a z$

$x^{2} + z^{2} - 2 a z = 0 x^{2} + z^{2} - 2 a z + a^{2} = a^{2}$

Выделим полный квадрат:

$x^{2} + (z - a)^{2} = a^{2}$

Это уравнение задаёт цилиндр c осью, совпадающей с координатной осью $y$ , и поднятый на $a$ по оси $z$ Ж

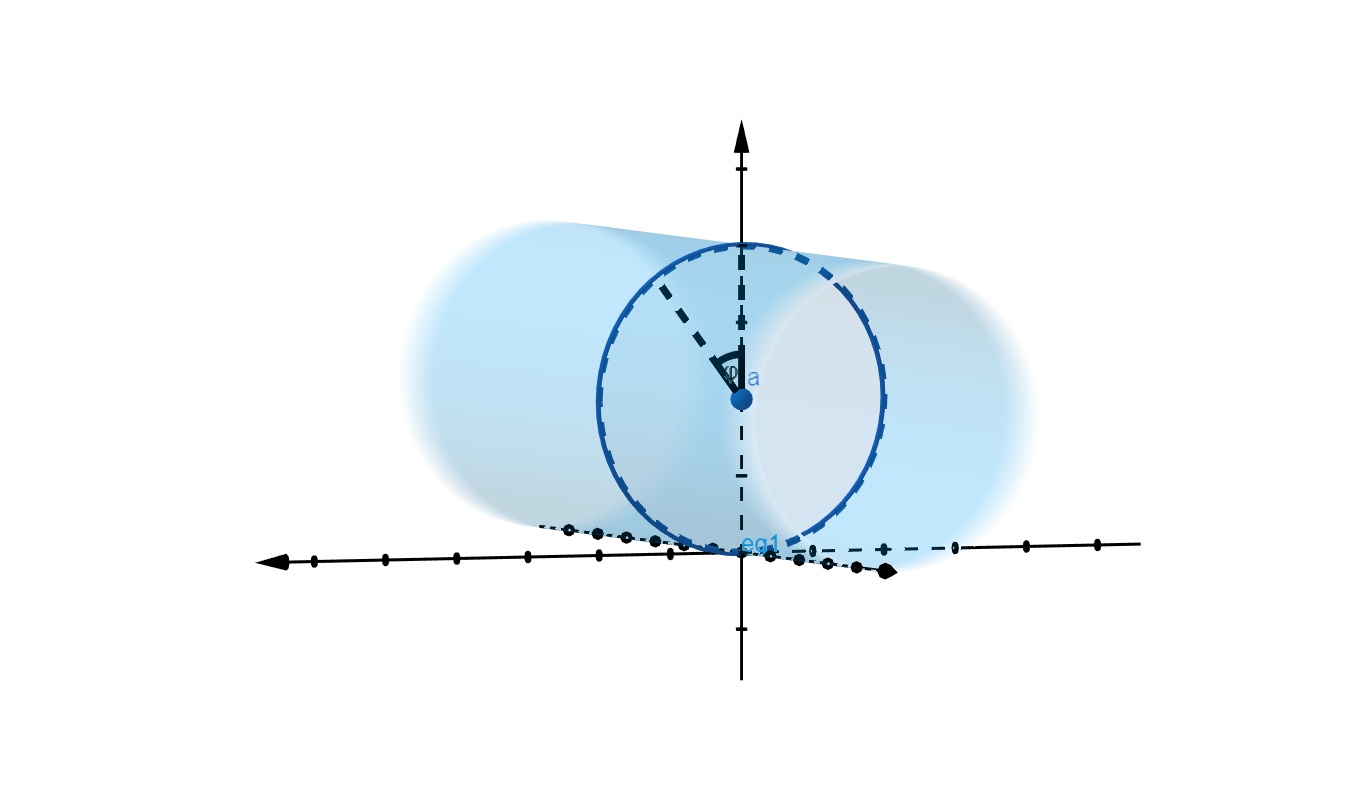
Иллюстрация 1

Введём смещённые цилиндрические координаты:

$x = a sin (φ) y = y z = a + a cos (φ)$

Элемент площади $d S = EG - F^{2} d φ d y$ :

$E = (\frac{\partial x}{\partial φ})^{2} + (\frac{\partial y}{\partial φ})^{2} + (\frac{\partial z}{\partial φ})^{2} = a^{2} cos^{2} (φ) + 0 + a^{2} sin^{2} (φ) = a^{2} (cos^{2} (φ) + sin^{2} (φ)) = a^{2}$

$F = \frac{\partial x}{\partial φ} \cdot \frac{\partial x}{\partial y} + \frac{\partial y}{\partial φ} \cdot \frac{\partial y}{\partial y} + \frac{\partial z}{\partial φ} \cdot \frac{\partial z}{\partial y} = 0 + 0 + 0 = 0$

$G = (\frac{\partial x}{\partial y})^{2} + (\frac{\partial y}{\partial y})^{2} + (\frac{\partial z}{\partial y})^{2} = 0 + 1 + 0 = 0$

$d S = EG - F^{2} d φ d y = a^{2} \cdot 1 + 0 = a$

Найдём граничные условия для $y$ из условия $z = x^{2} + y^{2}$ .

Так как $z > 0$ возведём в квадрат:

$z^{2} = x^{2} + y^{2} y^{2} = z^{2} - x^{2} y = \pm z^{2} - x^{2}$

Подставим введёную параметризацию:

$y = \pm (z^{2} - x^{2}) = \pm (a - a cos (φ))^{2} - (a sin (φ))^{2} = \pm a^{2} + 2 a^{2} cos (φ) + a^{2} cos^{2} (φ) - a^{2} sin^{2} (φ) = \pm a 1 + 2 cos (φ) + cos^{2} (φ) - sin^{2} (φ) = \pm a 1 + 2 cos (φ) + cos^{2} (φ) - (1 - cos^{2} (φ)) = \pm a 2 cos (φ) + 2 cos^{2} (φ) = \pm 2 a cos (φ) (cos (φ) + 1)$

Таким образом верхняя граница для $y$ :

$y = 2 a cos (φ) (cos (φ) + 1)$

Нижняя:

$y = - 2 a cos (φ) (cos (φ) + 1)$

Теперь найдём границы для $φ$ . Для этого рассмотрим проекцию на плоскость $XOZ$ :

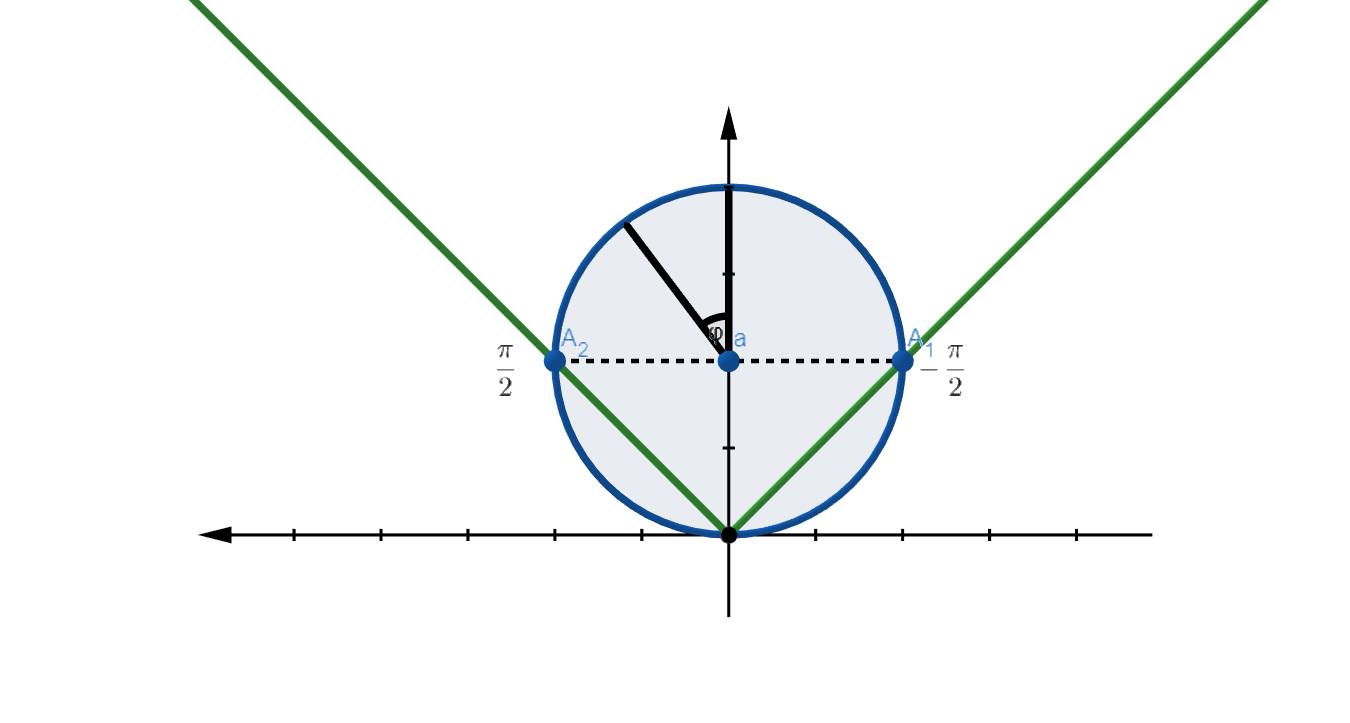
Иллюстрация 2

Проекция $x^{2} + z^{2} = 2 a z$ — окружность $x^{2} + (z - a)^{2} = a^{2}$ , а $z = x^{2} + y^{2}$ – $z ⩽ ∣ x ∣$ .

Найдём точки пересечения этих графиков (для поиска точек пересечения нужен график $z = ∣ x ∣$ ). Для этого раскорем модуль и решим две системы уравнений:

${x^{2} + (z - a)^{2} = a^{2} z = x {x^{2} + (z - a)^{2} = a^{2} z = - x$

Рассмотрим решение только первой системы уравнений, второе решается абсолютно аналогично. Подставим второе уравнение в первое:

$x^{2} + (x - a)^{2} = a^{2} 2 x^{2} - 2 a x + a^{2} = a^{2} 2 x^{2} - 2 a x = 0 x (x - a) = 0$

Откуда $x_{1}_{1} = 0$ и $x_{1}_{2} = a$ . Из второго уравнения $z_{1}_{1} = 0$ и $z_{1}_{2} = a$ .

Аналогично для второй системы $x_{2}_{1} = 0$ , $x_{2}_{2} = - a$ , $z_{2}_{1} = 0$ , $z_{2}_{2} = a$ .

Таким образом имеется три точки пересечения:

$A_{1} = (a, a) A_{2} = (- a, a) O = (0, 0)$

Центр окружности $x^{2} + (z - a)^{2} = a^{2}$ лежит на одной прямой с $A_{1}$ и $A_{2}$ . Значит угол $φ$ меняется от $- \frac{π}{2}$ до $\frac{π}{2}$ .

Используя всё, что было получено на предыдущих шагах перейдём от исходного поверхностного интеграла первого рода к повторному: $\iint_{s} z d S = \iint_{s^{'}} (a + a cos (φ)) a d φ d y = \int_{- \frac{π}{2}}^{\frac{π}{2}} d φ \int_{- 2 a c o s (φ) (c o s (φ) + 1)}^{2 a c o s (φ) (c o s (φ) + 1)} (a + a cos (φ)) a d y = \int_{- \frac{π}{2}}^{\frac{π}{2}} a (a + a cos (φ)) \int_{- 2 a c o s (φ) (c o s (φ) + 1)}^{2 a c o s (φ) (c o s (φ) + 1)} d y = \int_{- \frac{π}{2}}^{\frac{π}{2}} a (a + a cos (φ)) 22 a cos (φ) (cos (φ) + 1) = 22 a^{3} \int_{- \frac{π}{2}}^{\frac{π}{2}} cos (φ) (1 + cos (φ))^{3} d φ = 22 a^{3} \int_{- \frac{π}{2}}^{\frac{π}{2}} cos (φ) (1 + cos (φ))^{3} \frac{s in ( φ )}{s in ( φ )} d φ = 22 a^{3} \int_{- \frac{π}{2}}^{\frac{π}{2}} cos (φ) (1 + cos (φ))^{3} \frac{1}{s in ( φ )} d cos (φ) = 22 a^{3} \int_{- \frac{π}{2}}^{\frac{π}{2}} cos (φ) (1 + cos (φ))^{3} \frac{1}{1 - cos ^{2} ( φ )} d cos (φ) = 22 a^{3} \int_{- \frac{π}{2}}^{\frac{π}{2}} \frac{cos ( φ ) ( 1 + cos ( φ ) ) ^{3}}{( 1 - cos ( φ ) ) ( 1 + cos ( φ ) )} d cos (φ)$

Сделаем теперь замену переменных:

$t = cos (φ)$

Функция косинуса чётная и переодическая. Поэтому интеграл от $- \frac{π}{2}$ до $\frac{π}{2}$ можно представить как сумму двух интегралов от $- \frac{π}{2}$ до $0$ . Таким образом границы интегрирования после замены переменных станут от $cos (- \frac{π}{2}) = 0$ до $cos (0) = 1$ .

Продолжим с новой переменной:

$42 a^{3} \int_{0}^{1} \frac{t ^{\frac{1}{2}} ( 1 + t )}{( 1 - t ) ^{\frac{1}{2}}} d t = 42 a^{3} \int_{0}^{1} t^{\frac{1}{2}} (1 - t)^{- \frac{1}{2}} + t^{\frac{3}{2}} (1 - t)^{- \frac{1}{2}} = 42 a^{3} (B (\frac{3}{2}; \frac{1}{2}) + B (\frac{5}{2}; \frac{1}{2})) = 42 a^{3} (\frac{π}{2} + \frac{3 π}{8}) = \frac{7 2}{2} a^{3} π$

4298